Feedback Linearization - Its Performance and Limitations
The goal is to design a feedback control law that perfectly cancels the nonlinear term in the pendulum dynamics. For this simple example, the derivation is straightforward and the performance difference is easily observed.
We will start with the nonlinear model found in the post on State Space Model of a Pendulum as follows:
\begin{equation} \begin{alignedat}{1} \dot{x}_{1} &= x_{2} \\ \dot{x}_{2} &= -p \sin{x_{1}} + u \end{alignedat} \end{equation}The goal is to design an input $u$, that will cancel the nonlinear term $\sin{x_1}$ reducing the nonlinear system to a linear system after which a simple state feedback control law can be designed. Note that it is not always possible to cancel the nonlinear term, but in future posts, we will look at possible state transformations that allow for feedback linearization 1.
The uncertainty term $p$ will simulate modeling errors and we will look at its effects on the system's response.
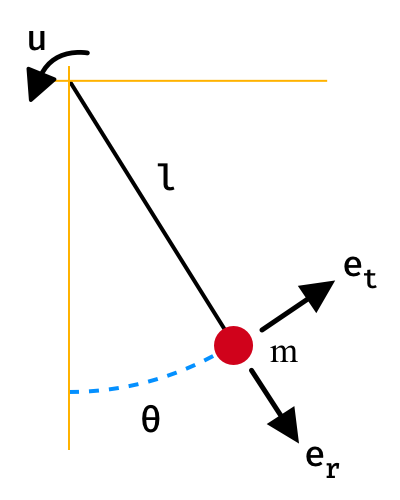
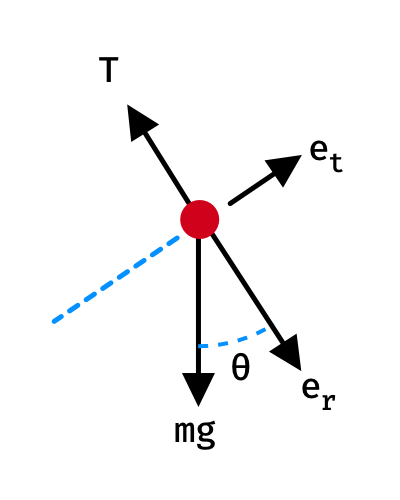
To find $u$ that cancels the nonlinear term, start with the given output equation $y=x_1$ and differentiate until the control input $u$ appears:
\begin{equation} \begin{alignedat}{1} y &= x_1 \\ \dot{y} &= \dot{x_1} = x_2 \\ \ddot{y} &= \ddot{x_1} = \dot{x_2} = -p\sin{x_1} + u \\ \end{alignedat} \end{equation}Note that $v$ is the synthetic input that we define as $v=\ddot{y}$ and will be used to design the state feedback control law. It follows that:
\begin{equation} \begin{alignedat}{1} u &= \hat{p}\sin{x_1} + v \\ \end{alignedat} \end{equation}Where $\hat{p}$ is an estimate or initial value of $p$ and will be used to introduce errors in modeling.
Substituting $u$ back into the dynamics results in:
\begin{equation} \begin{alignedat}{1} \dot{x}_{1} &= x_{2} \\ \dot{x}_{2} &= (\hat{p} - p)\sin{x_1} + v \end{alignedat} \end{equation}Notice that when $\hat{p}=p$ then we have perfect cancellation of the nonlinear term, resulting in a linear system. When $\hat{p}$ deviates, we will start to see the effects of the nonlinear term in the system's response.
Assuming perfect cancellation, we design $v$ to stabilize the linear system using state feedback.
\begin{equation} \begin{alignedat}{1} v &= -Kx \\ \end{alignedat} \end{equation}And the final dynamics equations with control input:
\begin{equation} \begin{alignedat}{1} \dot{x}_{1} &= x_{2} \\ \dot{x}_{2} &= (\hat{p} - p)\sin{x_1} - Kx \end{alignedat} \end{equation}Simulink Model
We will build off of the Simulink model from a previous post for simulating nonlinear dynamics using a state feedback controller.
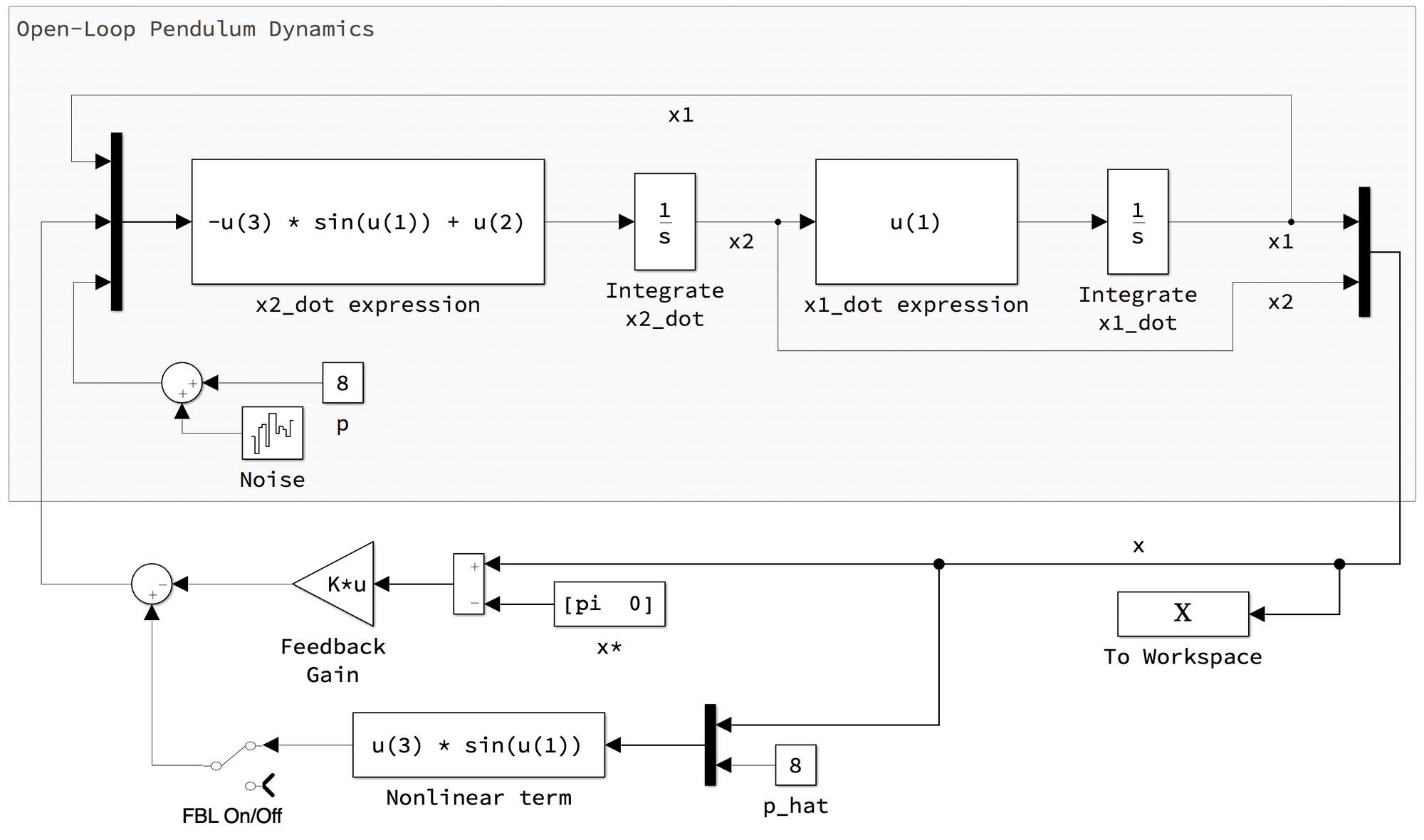
Simulations
We will stabilize the system around $(\pi, 0)$ (inverted pendulum position). This first simulation will use gains that purposely too low but will eventually stabilize the system. The reason for this extreme case is to clearly show the effects of feedback linearization. In both simulations, noise is added so that $(\hat{p} - p) \ne 0$ resulting in some, but not exact cancellation of the nonlinear term.
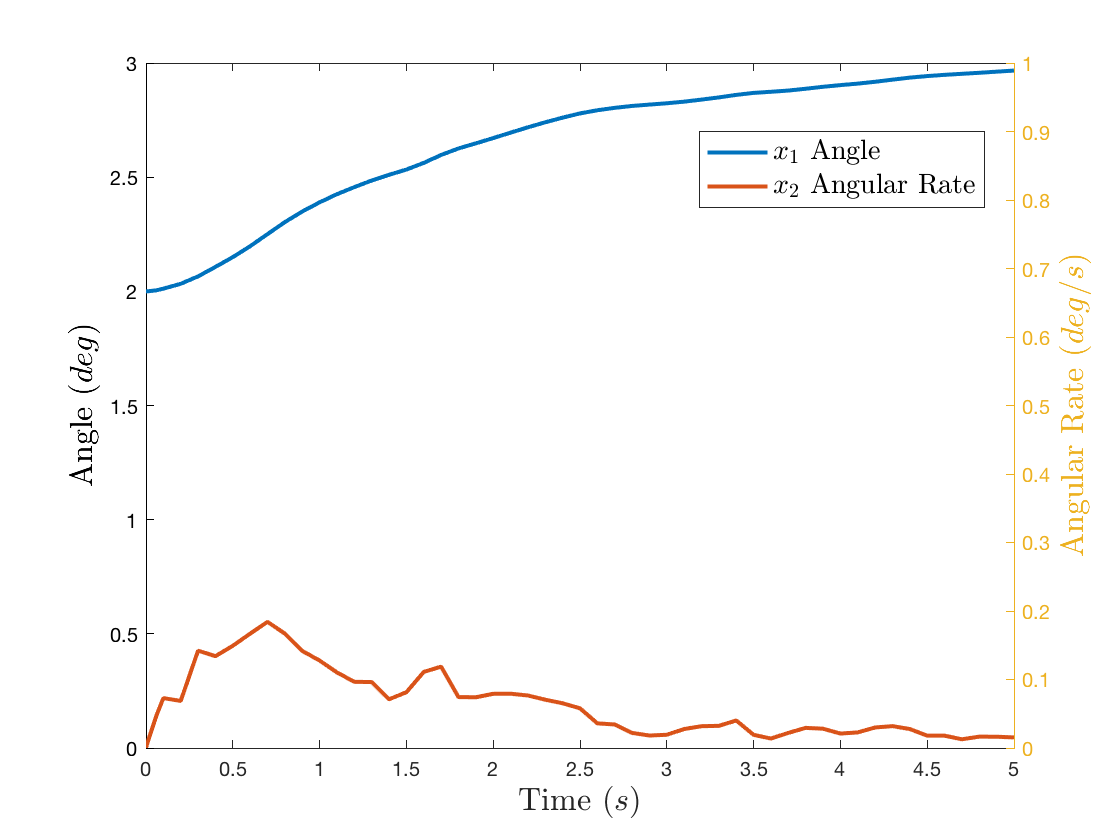
Note that with enough gain, in this example, the nonlinear term can be overcome, but to better show the effects of FBL, the gains used in the above simulation are $k_1 = 9, k_2 = 4$ and will remain constant for both cases.
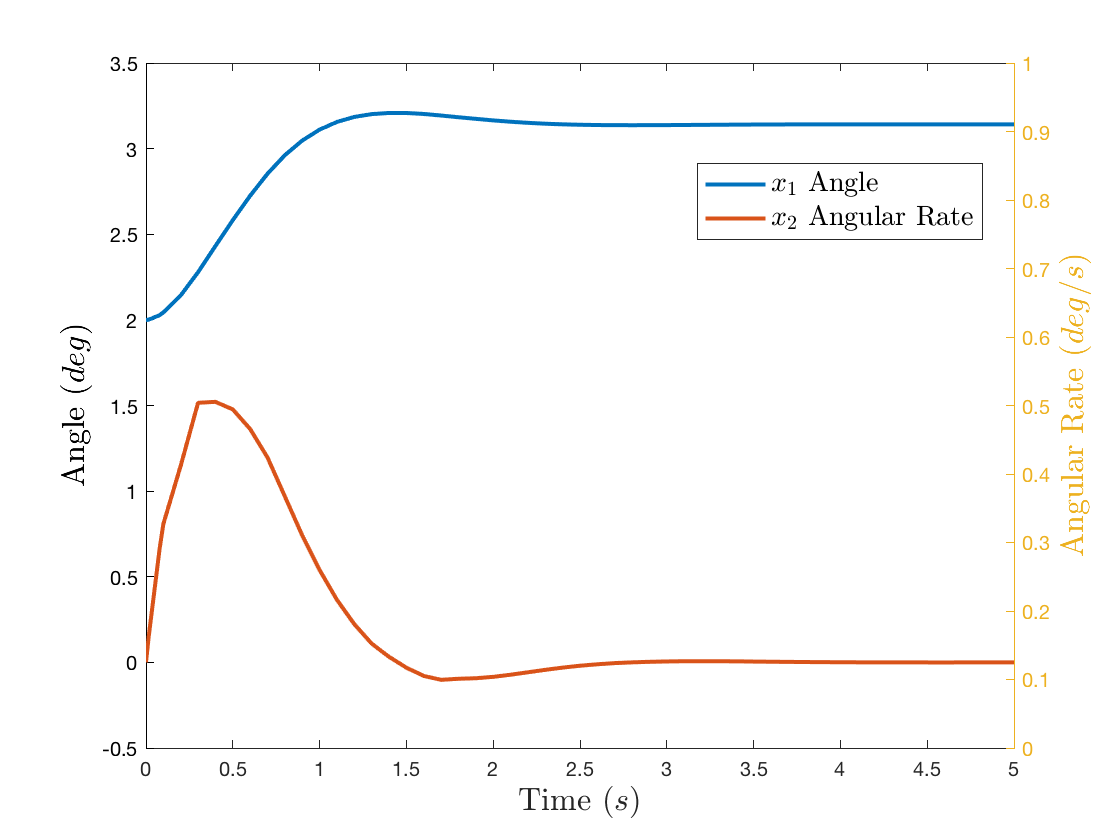
Notice that under the same insufficient feedback gains, the response is much better and similar to the previously tested linearized system.
For this simple system, it's easy to see how one might design a feedback linearizing control law, but many systems are not obvious or even possible unless transformed using a change of variable 1.
The Simulink model and MATLAB code for Feedback Linearization is available for download so you can try different control gains and parameters.
References
- Hassan K. Khalil, "Nonlinear Systems Third Edition," Prentice Hall, Upper Saddle River, New Jersey 07458, 2002
- Jean-Jacques E. Slotine and Weiping Li, "Applied Nonlinear Control," Prentice Hall, Englewood Cliffs, New Jersey 07632, 1991
