Brain-Computer Interface: Motor Neuron Simulation
Movements of the human body have been shown to correlate to neurons in the motor cortex of the brain and spinal cord.

These neurons are directionally tuned to produce the desired movement of the limb. Monitoring of motor neurons reveals that the firing rate is proportional to the direction of movement. The firing rate is at a maximum when the movement is in alignment with the cells preferred direction is proportional to the cosine of angle between the line of action and a cells preferred direction. Using this information a brain-computer interface is designed to calibrate and decode firing rates of selected neurons in the motor cortex. [1]
Introduction
An implantable device in the brain can simultaneously read 1,000 motor neuron firing rates. These are averaged while the patient imagines a position in the horizontal plane. The plane in front of the patient spans $0^{\circ}$ to $180^{\circ}$ at shoulder height. Using calibration data and the concept of directional tuning, a brain computer interface (BCI) takes firing rate input and predicts the imagined movement. Calibration of the device requires the patient to carry out predefined tasks, after which decoding and prediction can take place.
Brain-Computer Interface
The strategy outlined in [1] uses the concept of directionally tuned motor neurons and population vector analysis. When a movement is executed or imaged, the neurons in the motor cortex fire in their preferred direction. However, the fire rate is modulated by the angle of the movement with respect to the cells preferred angle. This observation allows one to formulate a weighted vector sum that points in the direction of the desired movement. The weight of each vector is proportional to the difference between the movement direction and the cells preferred direction. The strategy is outlined in the diagram below. [1]
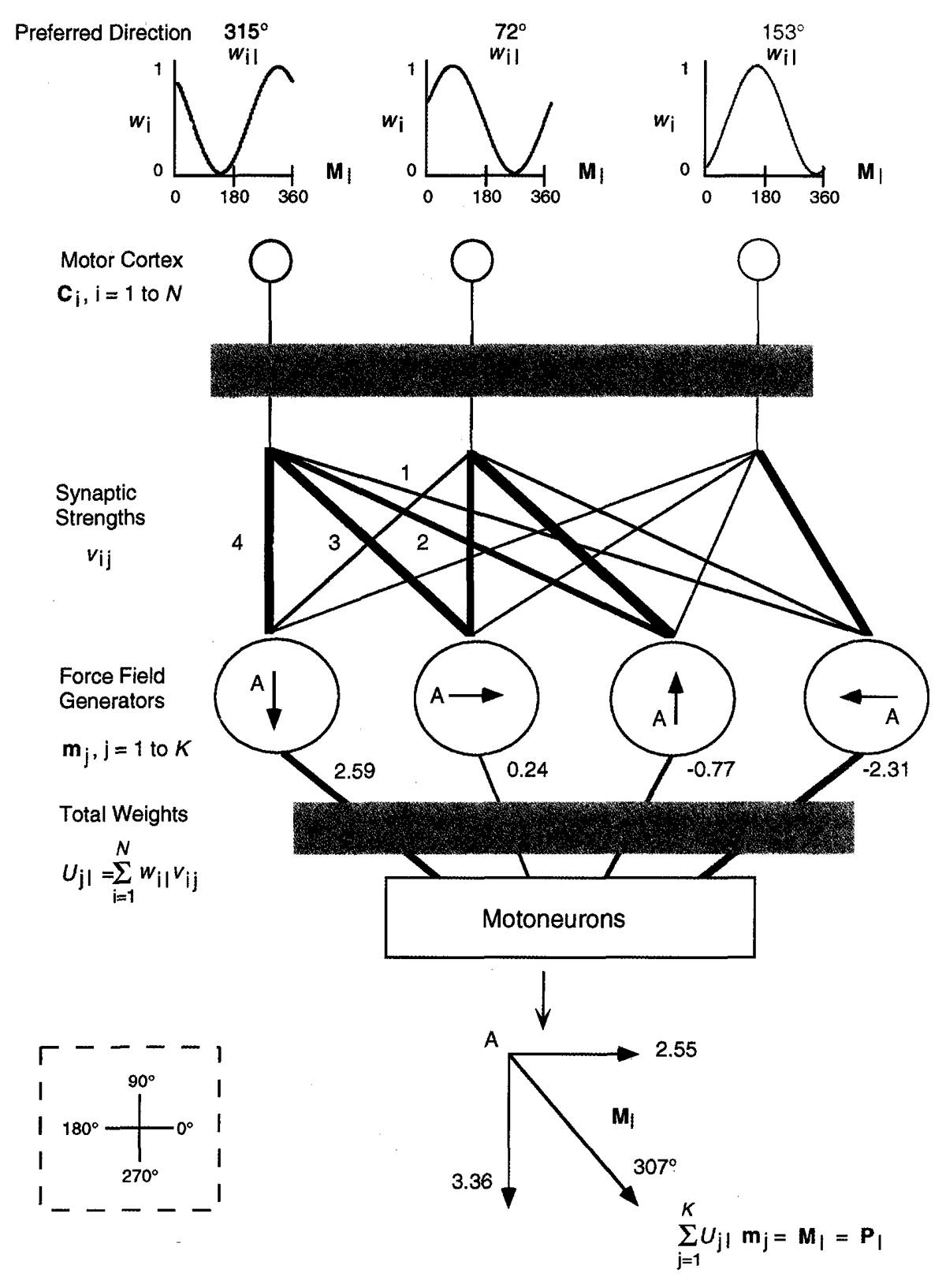
The population vector is defined as: $P_{l}=\sum _{ i }^{ N }{ w_{il} }$ where $P_{l}$ is the vector pointing in the direction of movement $l$.
During decoding the population vector is combined with: $\sum _{ j=1 }^{ K }{ U_{jl}m_{j} }=P_{l}$. The predicted movement is obtained by solving the equations above using the calculated values of $w_{il}$, $U_{jl}$ and $P_{l}$.
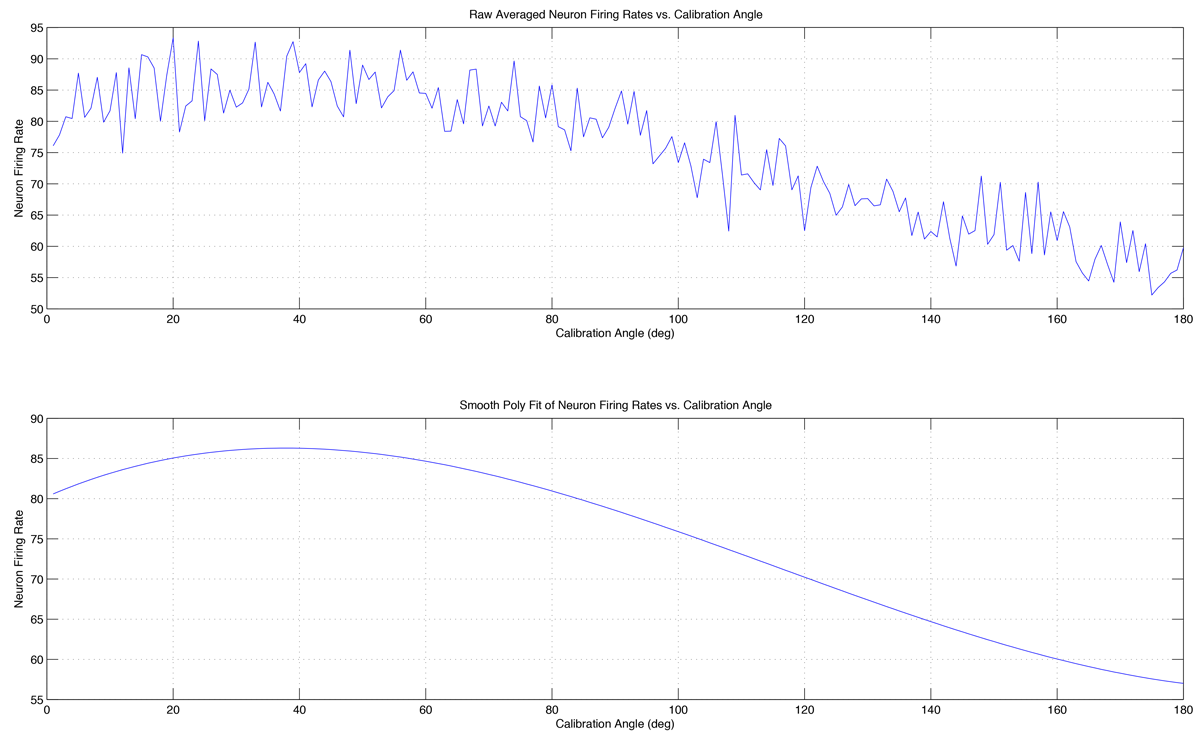
Calibration is carried out by having the patient imagine moving their arm in a full $180^{\circ}$ sweep in front of them. The BCI records the firing rates of all the neurons at incremental angles and determines each cells' preferred direction (MATLAB code for Calibration in the appendix). Firing rate information is logged throughout the sweep and a curve fit is applied to the data as can be seen in figure 2.
Movements are not entirely controlled by the motor cortex, signals from the brain activate motoneurons through the spinal cord and then ultimately muscle actuation results. Since this process partly bypasses the brain, measurements of motoneurons in the brain may not accurately represent the intended movement. In addition, research suggests that influences from activated neurons may spread across multiple populations that are not measured. [1]
The directionally tuned behavior of neurons in the motor cortex allow for a straight forward approach to decoding using population vectors. Neuron firing rate is at a maximum in its preferred direction and proportionally decreases as a function of the diverging angle. Using the approach presented, neurons in the motor cortex can be monitored and a weighted average of the direction vectors can be calculated. This population vector can be used to determine the overall indented movement, and optimizing for the number of measured neurons may increase decoding efficiency and accuracy.
References
- Georgopoulos, A. P., ``On the Translation of Directional Motor Cortical Commands to Activation of Muscles via Spinal Interneronal Systems," Cognitive Brain Research, 1996
